前言
典例剖析
例1【2019届高三理科数学三轮模拟训练用题】定义:椭圆\(\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1(a>b>0)\)中长度为整数的焦点弦(过焦点的弦)为“好弦”,则椭圆\(\cfrac{x^2}{25}+\cfrac{y^2}{9}=1\)的所有“好弦”的长度为【】
分析:椭圆\(\cfrac{x^2}{25}+\cfrac{y^2}{9}=1\)中的最短弦长为通经,最长的弦长为长轴的长,容易计算得到通经长为\(\cfrac{18}{5}=3.6\),则椭圆的弦从最短的弦变化为最长的弦的过程中,得到的好弦的长度分别为\(4\),\(5\),\(6\),\(7\),\(8\),\(9\),\(10\),
而且由于椭圆关于\(x\)轴对称,故有两组,又由于焦点有两个,故还有两组,故共有四组,其和为\((4+5+6\) \(+7+8+9+\) \(10)\times 4\) \(=196\),但是上述的计算过程中将最长的好弦(即长轴)多计算了3次,故所求为\(196-30=166\),故选\(B\)。
例2【2015\(\cdot\)全国卷Ⅰ】
在平面四边形\(ABCD\)中,\(\angle A=\angle B=\angle C=75^{\circ}\),\(BC=2\),则\(AB\)的取值范围是___________。
分析:本题目非常特别,依据题意我们做出的图形是平面四边形,
当我们将边\(AD\)平行移动时,题目的已知条件都没有改变,故想到将此静态图变化为动态图,
平行移动\(AD\)时,我们看到了两个临界位置,即四边形变化为三角形的两个状态,
其一是四边形变化为三角形\(ABF\),此时应该有\(BF<AB\);
其二是四边形变化为三角形\(ABE\),此时应该有\(BE>AB\);
故动态的边\(AB\)的范围是\(BF<AB<BE\),从而求解。
解答:如图所示,延长\(BA\)与\(CD\)交于\(E\),过\(C\)做\(CF//AD\)交\(AB\)于\(F\),则\(BF<AB<BE\);
在等腰三角形\(CFB\)中,\(\angle FCB=30^{\circ}\),\(CF=BC=2\),由余弦定理得到\(BF=\sqrt{6}-\sqrt{2}\);
在等腰三角形\(ECB\)中,\(\angle CEB=30^{\circ}\),\(\angle ECB=75^{\circ}\),\(BE=CE,BC=2\),
由正弦定理得到\(BE=\sqrt{6}+\sqrt{2}\);
故\(\sqrt{6}-\sqrt{2}<AB<\sqrt{6}+\sqrt{2}\)
解后反思引申:
1、求\(CD\)的取值范围;
分析:由上述的动态图可知,\(0<CD<CE=BE=\sqrt{6}+\sqrt{2}\);
2、求\(AD\)的取值范围;
分析:由上述的动态图可知,\(0<AD<CF=BC=2\);
3、求四边形\(ABCD\)的周长的取值范围;
分析:四边形\(ABCD\)的周长介于\(\Delta BCF\)的周长和\(\Delta BCE\)的周长之间,
故其取值范围是\((4+\sqrt{6}-\sqrt{2},2(\sqrt{6}+\sqrt{2})+2)\);
4、求四边形\(ABCD\)的面积的取值范围;
分析:四边形\(ABCD\)的面积介于\(\Delta BCF\)的面积和\(\Delta BCE\)的面积之间,
\(S_{\Delta BCF}=\cfrac{1}{2}\times 2\times 2\times sin30^{\circ}=1\);
\(S_{\Delta BCE}=\cfrac{1}{2}\times (\sqrt{6}+\sqrt{2})\times (\sqrt{6}+\sqrt{2})\times sin30^{\circ}=2+\sqrt{3}\);
故其取值范围是\((1,2+\sqrt{3})\);
例3【2019高三理数二轮专题训练题】在\(\triangle ABC\)中,\(AB=AC=2\sqrt{2}\),\(\overrightarrow{DB}=3\overrightarrow{AD}\),连接\(CD\)并取线段\(CD\)的中点为\(F\),则\(\overrightarrow{AF}\cdot \overrightarrow{CD}\)的值为________。
法1:常规方法,基向量法,由于\(\overrightarrow{DB}=3\overrightarrow{AD}\),线段\(CD\)的中点为\(F\),则\(\overrightarrow{CD}=\cfrac{1}{4}\overrightarrow{AB}-\overrightarrow{AC}\),
\(\overrightarrow{AF}=\cfrac{1}{4}\overrightarrow{AB}+\cfrac{1}{2}\overrightarrow{DC}=\cfrac{1}{4}\overrightarrow{AB}+\cfrac{1}{2}(\overrightarrow{AC}-\cfrac{1}{4}\overrightarrow{AB})=\cfrac{1}{4}\overrightarrow{AB}+\cfrac{1}{2}\overrightarrow{AC}=\cfrac{1}{2}(\cfrac{1}{4}\overrightarrow{AB}+\overrightarrow{AC})\),
则\(\overrightarrow{AF}\cdot \overrightarrow{CD}=\cfrac{1}{2}(\cfrac{1}{16}{\overrightarrow{AB}}^2-\overrightarrow{AC}^2)=\cfrac{1}{2}(\cfrac{1}{16}\times 8-8)=-\cfrac{15}{4}\)
法2:特殊化策略,当\(\triangle ABC\)为等边三角形,或是等腰直角三角形时,题目中的条件仍然不变化,故可以采用特殊化策略,
比如\(\triangle ABC\)为等腰直角三角形,以\(A\)为坐标原点建系,然后利用相应点的坐标计算。提示:\(-\cfrac{15}{4}\)
例4【2019高三理数三轮模拟训练题】设点\(M\)在直线\(l:y=kx+1\) \((k为常数)\)上运动,过点\(M\)作圆\(C:(x-2)^2+(y-1)^2=1\)的切线,切点为\(N\),当切线长\(|MN|\)取得最小值时,点\(M\)的横坐标为\(\cfrac{2}{5}\),则常数\(k\)的值为【】
法1:用动态图形观察得到切线长的最小值;作出如图所示的示意图,当点\(M\)向圆靠近时,切线的长度逐渐变小,当点\(M\)落在点\(P\)时(点\(P\)为圆心点\(O\)在直线\(l\)上的垂足),切线长\(|MN|\)取得最小值,
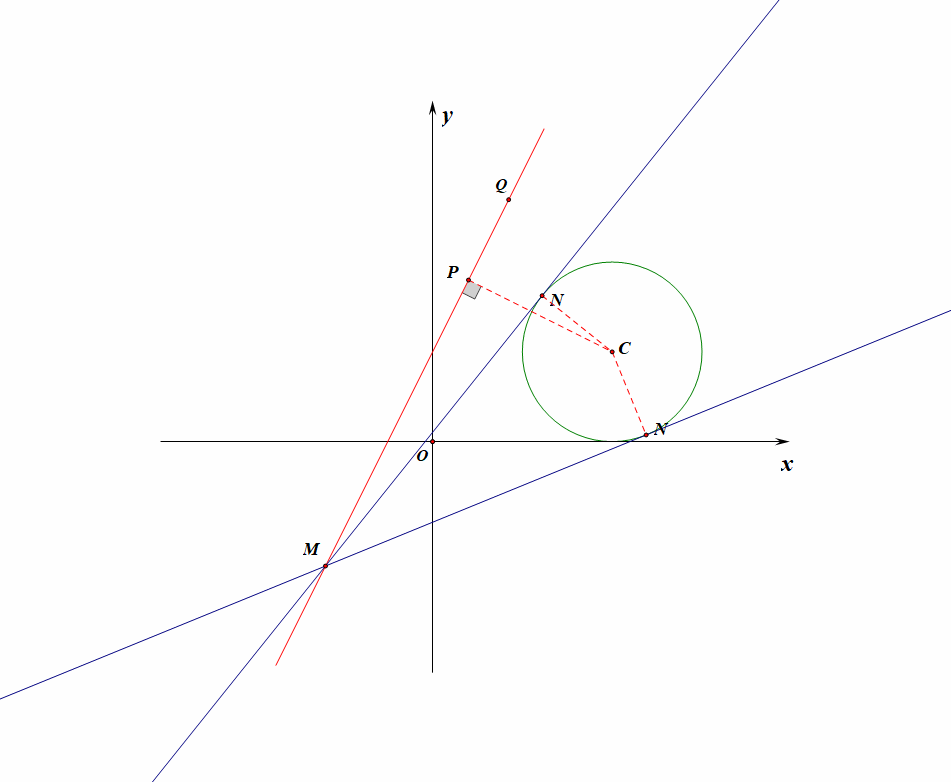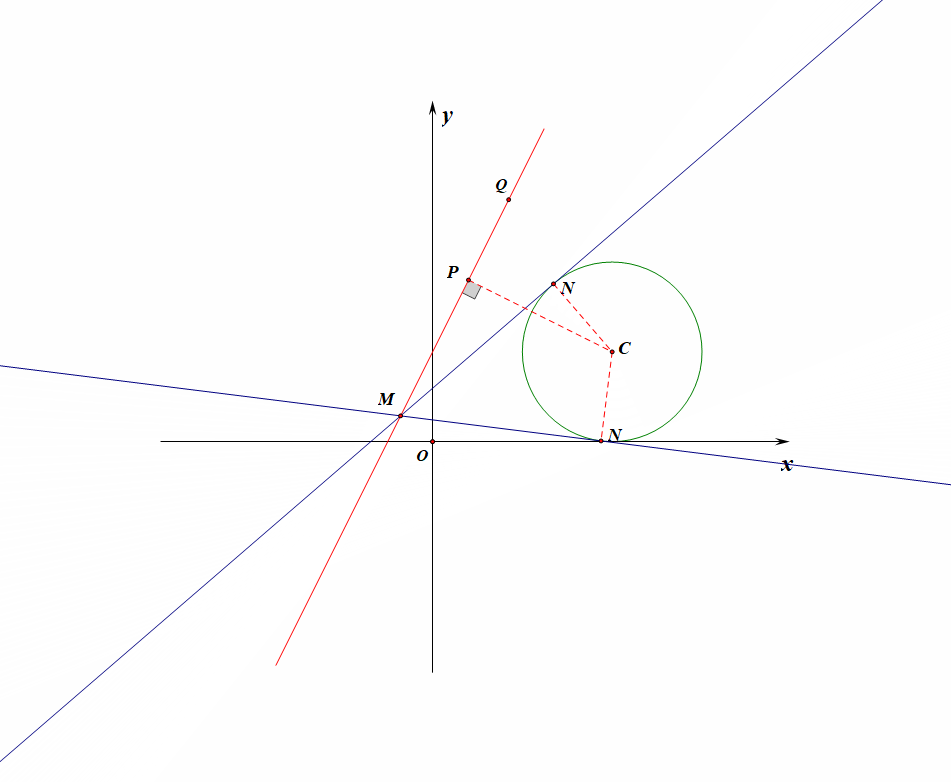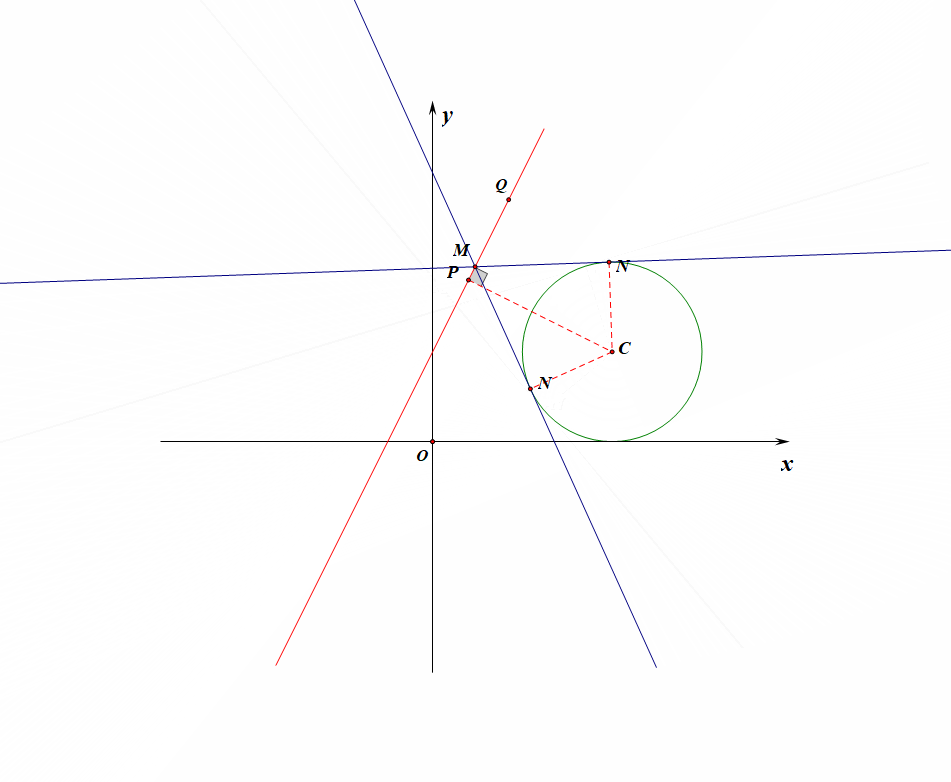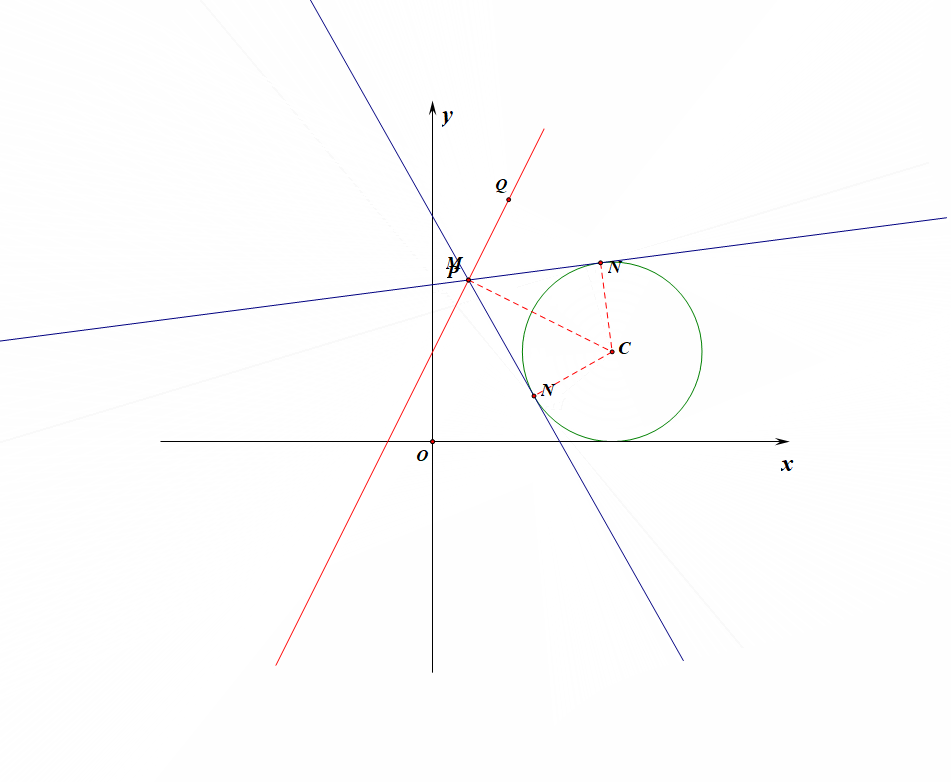
此时直线\(CP:y-1=-\cfrac{1}{k}(x-2)\)②,和\(l:y=kx+1\)①联立,消去\(y\),再将\(x=\cfrac{2}{5}\)代入,求得\(k=\pm 2\),故选\(D\)。
法2:先判断当切线\(MN\)最短时,点\(M\)位于点\(P\)处,令\(M(\cfrac{2}{5},y)\),
则\(k_l=\cfrac{y-1}{\frac{2}{5}}\),\(k_{OM}=\cfrac{y-1}{\frac{2}{5}-1}\),由于\(k_l\cdot k_{OM}=-1\),解得\(y=1\pm \cfrac{4}{5}\),
当\(y=1+\cfrac{4}{5}=\cfrac{9}{5}\)时,\(k=\cfrac{y-1}{\frac{2}{5}}=2\),当\(y=1-\cfrac{4}{5}=\cfrac{1}{5}\)时,\(k=\cfrac{y-1}{\frac{2}{5}}=-2\),
即\(k=\pm 2\),故选\(D\)。
法3:用计算的方法得到切线长的最小值;设\(M(\cfrac{2}{5},y)\),
则\(|MN|^2=(\cfrac{2}{5}-2)^2+(y-1)^2-1^2=(y-1)^2+\cfrac{39}{25}\),此法错误,原因是在此题目中\(y\)是定值,不是变量;如果将\(y\)替换为\(kx+1\),然后求解就是正确的。
法4:用计算的方法得到切线长的最小值;设\(M(x,kx+1)\),\(O(2,1)\)
则\(|MN|^2=(x-2)^2+(kx+1-1)^2-1^2=k^2x^2+x^2-4x+3\)
\(=(k^2+1)x^2-4x+3=(k^2+1)[x^2-\cfrac{4}{k^2+1}x+(\cfrac{2}{k^2+1})^2]+3-\cfrac{4}{k^2+1}\),
\(=(k^2+1)(x-\cfrac{2}{k^2+1})^2+3-\cfrac{4}{k^2+1}\),
当\(x=\cfrac{2}{k^2+1}\)时,\(|MN|\)最小,且此时\(x=\cfrac{2}{5}\),
由\(\cfrac{2}{5}=\cfrac{2}{k^2+1}\),解得\(k=\pm 2\),故选\(D\)。
例5【2019高三理数三轮模拟训练题】如图,已知正方体\(ABCD-A_1B_1C_1D_1\)中,\(E\)是\(AB\)的中点,点\(F\)在对角线\(BD_1\)上运动,设直线\(EF\)与底面\(ABCD\)所成角为\(\theta\),则\(\theta\)的最大值为【】
法1:运用运动变化的观点来求解,连结\(BD\),过点\(F\)作\(FG\perp BD\)于点\(G\),连结\(EG\),则\(\angle GEF=\theta\),我们容易看到当点\(F\)从点\(B\)开始向点\(D_1\)运动时,\(\theta=0\),可以猜想整个过程中,\(\theta\)是逐渐增大的,至于具体的增大是以什么样的函数形式增大,我们目前是不知道的,不过我们可以通过运动过程知道,选项\(A\)和选项\(B\)肯定是错误的。
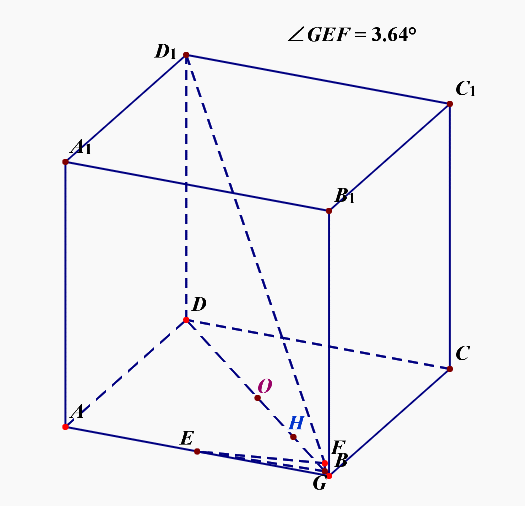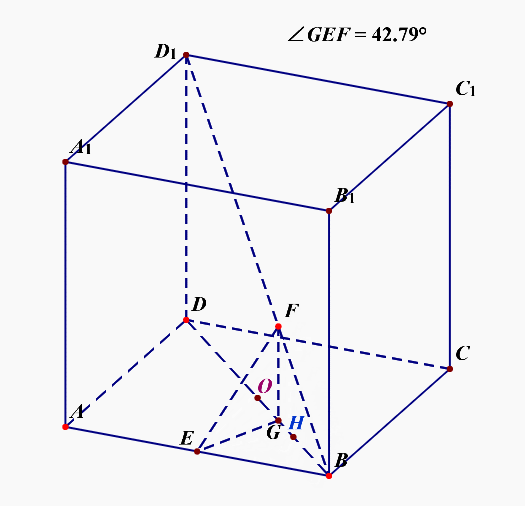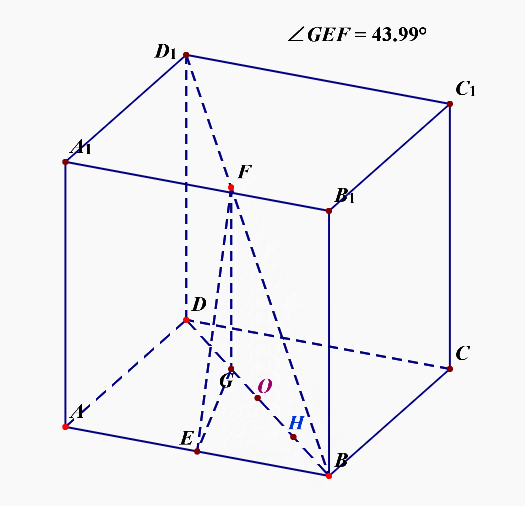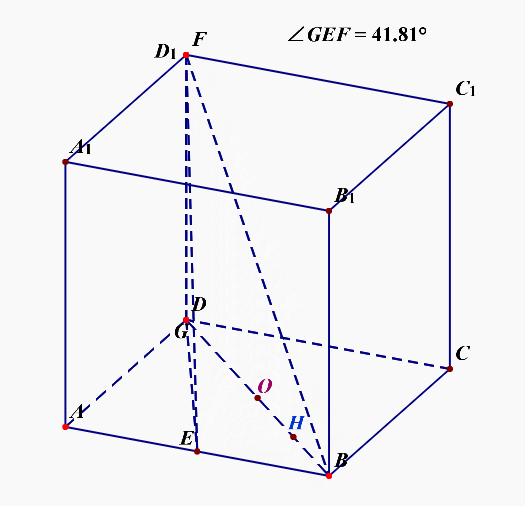
接下来,需要我们分析几个特殊位置,其一点\(G\)落在点\(H\)处(其中\(EH\perp BD\)),其二点\(G\)落在点\(O\)处(其中\(O\)是下底面的中心),其三点\(G\)落在点\(D\)处,
当点\(G\)落在点\(D\)处时,设棱长为2,可以知道\(EG=\sqrt{5}\),\(FG=2\),故\(tan\theta=\cfrac{2}{\sqrt{5}}\),结合选项,这种情况排除,也说明整个运动过程不是一直增大的;
当点\(G\)落在点\(O\)处时,可以知道\(EG=1\),\(FG=1\),故\(tan\theta=1\),即\(\theta=\cfrac{\pi}{4}\);
当点\(G\)落在点\(H\)处时,可以知道\(EG=\cfrac{\sqrt{2}}{2}\),\(FG=\cfrac{1}{2}\),故\(tan\theta=\cfrac{\sqrt{2}}{2}\),此时\(\theta<\cfrac{\pi}{4}\)。
结合以上情形可知,应该选\(D\)。
【解后反思】如果我们还需要将本题目的整个运动过程都弄清楚,可以借助函数来思考,比如还是设棱长为2,设\(BG=t\),则\(t\in [0,2\sqrt{2}]\),
则由\(\triangle BGF\sim \triangle BDD_1\),可得到\(\cfrac{t}{2\sqrt{2}}=\cfrac{FG}{2}\),则\(|FG|=\cfrac{\sqrt{2}}{2}t\),
则在\(\triangle BGE\)中,\(|BG|=t\),\(|BE|=1\),\(\angle EBG=45^{\circ}\),则由余弦定理可知,
\(|EG|^2=1+t^2-2\cdot 1\cdot t\cdot cos45^{\circ}=t^2-\sqrt{2}t+1\),在\(Rt\triangle EFG\)中,
则\(tan^2\theta=\cfrac{\frac{t^2}{2}}{t^2-\sqrt{2}t+1}=\cfrac{t^2}{2t^2-2\sqrt{2}t+2}=\cfrac{1}{2-\frac{2\sqrt{2}}{t}+\frac{2}{t^2}}\)
\(=\cfrac{1}{2(\frac{1}{t})^2-2\sqrt{2}\cdot \frac{1}{t}+2}=\cfrac{1}{2(\frac{1}{t}-\frac{\sqrt{2}}{2})^2+1}\),
当\(\cfrac{1}{t}=\cfrac{\sqrt{2}}{2}\)时,即\(t=\sqrt{2}\)时,\(tan^2\theta\)达到最大值\(1\),此时\(tan\theta\)也达到最大值\(1\),
则\(\theta=\cfrac{\pi}{4}\),且此时点\(G\)位于下底面的中点\(O\)处。故选\(D\).
例7【向量的投影的几何意义】【2018西安八校联考第5题】
已知\(O\)是坐标原点,点\(A(2,1)\),点\(M(x,y)\)是平面区域\(\begin{cases}&y\leq x\\&x+y\leq 1\\&y\ge -1\end{cases}\)内的一个动点,则\(\overrightarrow{OA}\cdot \overrightarrow{OM}\)的最大值是多少?
法1:利用向量的坐标运算得到,\(\overrightarrow{OA}\cdot \overrightarrow{OM}=2x+y\),故转化为求\(2x+y\)的最大值,即求\(z=2x+y\)的最大值,用线性规划的常规方法解决即可。
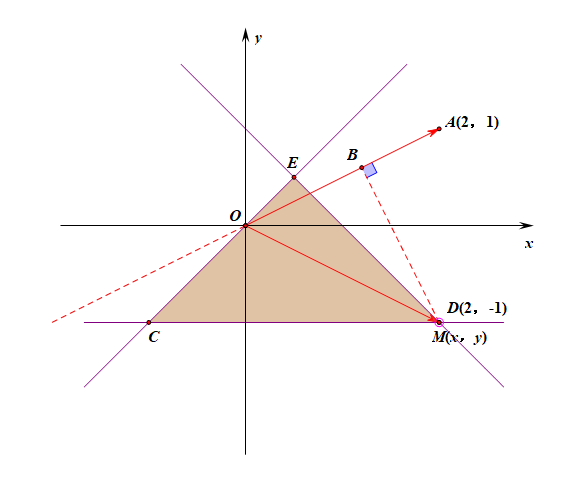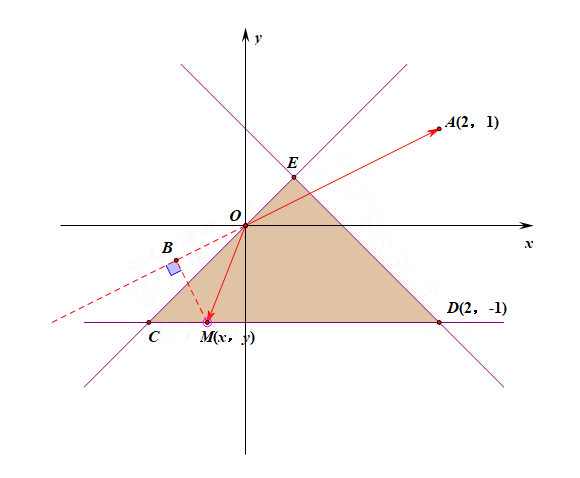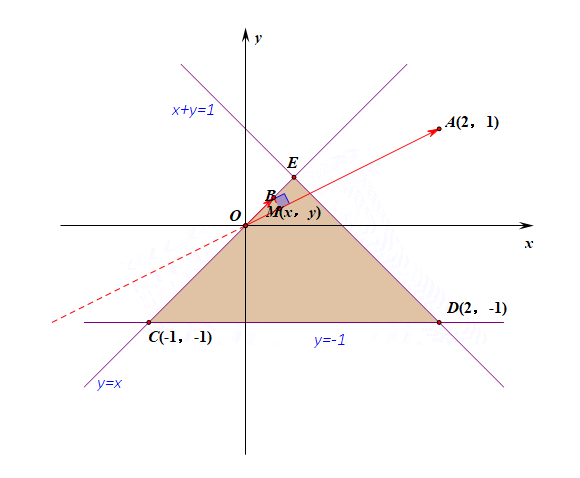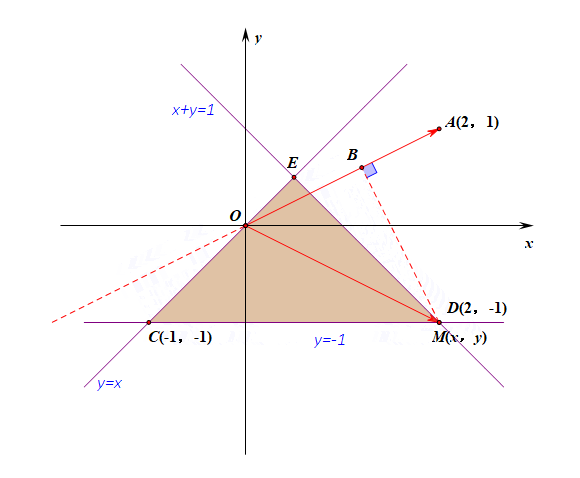
法2:利用向量的投影的几何意义求解,说明:点\(M\)是三角形区域内部及边界上的一个动点,动画只做了点\(M\)在边界上的情形;
注:图中有向线段\(OB\)是向量\(\overrightarrow{OM}\)在向量\(\overrightarrow{OA}\)方向上的投影,它是可正,可负,可零的;
\(\overrightarrow{OA}\cdot \overrightarrow{OM}=|\overrightarrow{OA}|\cdot |\overrightarrow{OM}|\cdot cos\theta\),其中\(|\overrightarrow{OA}|\)是个定值,
故只需要求\(|\overrightarrow{OM}|\cdot cos\theta\)的最大值,而\(|\overrightarrow{OM}|\cdot cos\theta\)的几何意义是\(\overrightarrow{OM}\)在\(\overrightarrow{OA}\)方向上的投影,
由图形可知,当点\(M(x,y)\)位于点\((2,-1)\)时投影\(|\overrightarrow{OM}|\cdot cos\theta\)最大,故将点\((2,-1)\)代入\(\overrightarrow{OA}\cdot \overrightarrow{OM}=3\)。
变式题1:求\(\overrightarrow{OA}\cdot \overrightarrow{OM}\)的最小值是多少?
分析:由上图可以看出,当两个向量的夹角为钝角时,其投影是负值,故当点\(M\)位于点\(C\)时,其内积最小,
此时将点\((-1,-1)\)代入得到\(\overrightarrow{OA}\cdot \overrightarrow{OM}=-3\)。
变式题2:求向量\(\overrightarrow{OM}\)的投影的绝对值最小时的动点\(M\)的轨迹方程?
分析:当其夹角为\(90^{\circ}\)时,有向线段\(OB=0\),故向量\(\overrightarrow{OM}\)的投影的绝对值最小\(0\);
此时,点\(M\)在三角形区域内部且和直线\(OA\)垂直,故其轨迹为\(y=-2x,(-1\leqslant y\leqslant 0)\)
例11【2019届高三理科数学第三轮模拟训练题】已知函数\(f(x)=lnx+2mx-2mx^2\)有两个不同的零点,则实数\(m\)的取值范围是【】
法1:先转化为函数\(y=g(x)=lnx\)和函数\(y=h(x)=2m(x^2-x)\)有两个交点的问题,在同一个坐标系中做出两个函数的图像,如下图所示:
我们先想着让\(m=0\),则此时两个函数的图像只有一个交点,当\(m>>0\)时,其有了两个交点,其中一个固定交点\((1,0)\),另外一个是变化的交点,当\(m\)逐渐增大时,变化的交点逐渐靠近固定的交点,最后合二为一,此时两条曲线相切于点\((1,0)\),当\(m\)再增大时,两个函数又有了两个交点;
接下来,只需要验证当切点为\((1,0)\)时,\(m\)应该等于多少即可;
由\(h'(x_0)=\cfrac{1}{x_0}=2m(2x_0-1)=g'(x_0)\),\(y_0=lnx_0\),\(y_0=2m(x_0^2-x_0)\),用点\((1,0)\)验证得到\(m=\cfrac{1}{2}\),故选\(B\)。